4. 라이브러리

4.1. NumPy 라이브러리

4.1.1. 넘파이 배열

4.1.1.1. 넘파이 배열 소개

NumPy
- Numerical Python의 약자로, C언어로 구현된 Python 라이브러리
- 고성능 수치 계산, 대규모 다차원 배열 및 행렬 연산에 최적화

넘파이 배열(ndarray)
- 리스트처럼 데이터를 모아 저장하는 자료구조
- 모든 원소가 동일한 자료형으로 저장(효율적인 메모리 관리 및 빠른 연산)
- 대규모 데이터 처리에 유리함
- 반복문 없이 배열 간 연산이 가능한 브로드캐스팅 및 벡터화 연산 지원
- 다양한 수학 함수, 선형대수, 난수 생성 기능 제공

4.1.1.2. 넘파이 배열 생성

함수	설명
np.array()	리스트, 튜플 등으로부터 배열 생성
np.zeros()	모든 값이 0인 배열 생성
np.ones()	모든 값이 1인 배열 생성
np.full()	지정한 값으로 이루어진 배열 생성
np.arange()	범위를 지정하여 연속적인 값의 배열 생성(`range()`와 비슷)
np.linspace()	시작과 끝을 기준으로, 지정한 개수만큼 일정 간격의 값으로 배열 생성
np.eye()	행과 열의 크기를 지정할 수 있는 단위행렬(2차원 배열) 생성
np.identity()	정방 단위행렬(2차원 배열) 생성

import numpy as np

# 넘파이 배열 생성1
arr1 = np.array([1, 2, 3])
arr2 = np.array((6, 7, 8, 9))
print(arr1)
print(arr2)

[1 2 3]
[6 7 8 9]

# 넘파이 배열 생성2
arr1 = np.zeros(5)
arr2 = np.ones(3)
arr3 = np.full(2, 5)
print(arr1)
print(arr2)
print(arr3)

[0. 0. 0. 0. 0.]
[1. 1. 1.]
[5 5]

# 넘파이 배열 생성3
arr1 = np.arange(10)
arr2 = np.arange(3, 6)
arr3 = np.arange(1, 11, 2)
arr4 = np.arange(0, 1, 0.1)
print(arr1)
print(arr2)
print(arr3)
print(arr4)

[0 1 2 3 4 5 6 7 8 9]
[3 4 5]
[1 3 5 7 9]
[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

# 넘파이 배열 생성4
arr = np.linspace(0, 1, 5)
print(arr)

[0.   0.25 0.5  0.75 1.  ]

# 넘파이 배열 생성5
arr1 = np.eye(3)
arr2 = np.eye(3, 4, k=1)
print(arr1)
print(arr2)

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
[[0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]

# 넘파이 배열 생성6 : np.identity()는 np.eye()의 특수한 경우
arr = np.identity(4)
print(arr)

[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]

4.1.1.3. 넘파이 배열 속성

속성	설명
.dtype	배열 원소의 자료형
.ndim	배열의 차원 수
.shape	배열의 모양(행, 열)
.size	배열의 전체 원소 개수
.itemsize	원소 하나의 메모리 크기

# 넘파이 배열 속성
arr = np.array([[1, 2, 3], [4, 5, 6]])       # 2차원 배열
print(arr)
print(arr.dtype)
print(arr.ndim)
print(arr.shape)
print(arr.size)
print(arr.itemsize)

[[1 2 3]
 [4 5 6]]
int32
2
(2, 3)
6
4

4.1.2. 차원과 축

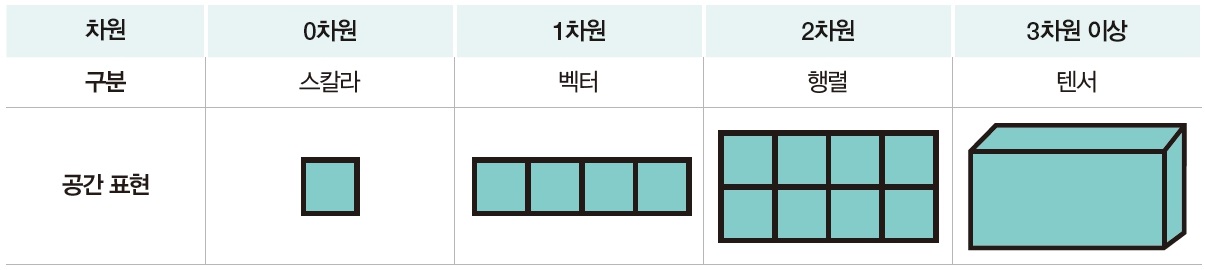
4.1.2.1. 차원(dimension)

넘파이 배열의 차원
- 관측하고자 하는 데이터의 속성의 수 또는 측정 항목의 수
- 스칼라(scalar) : 0차원 배열, 배열에서 값을 표현하는 가장 기본 단위로 하나의 실수를 저장할 수 있음
- 벡터(vector) : 1차원 배열, 스칼라 여러 개를 나열한 배열
- 행렬(matrix) : 2차원 배열, 1차원 배열을 여러 개 묶은 배열
- 텐서(tensor) : 3차원 이상의 배열, 벡터의 집합

arr0 = np.array(3.14)                        # 0차원 배열(스칼라)
arr1 = np.array([3.14])                      # 1차원 배열(벡터)
arr2 = np.array([[3.14]])                    # 2차원 배열(행렬)
arr3 = np.array([[[3.14]]])                  # 3차원 배열(텐서)

print(arr0.ndim, arr0.shape)
print(arr1.ndim, arr1.shape)
print(arr2.ndim, arr2.shape)
print(arr3.ndim, arr3.shape)

0 ()
1 (1,)
2 (1, 1)
3 (1, 1, 1)

# 1차원 배열(벡터)
arr = np.array([1, 2, 3])
print(arr.ndim)
print(arr.shape)

1
(3,)

# 2차원 배열(행렬)
arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr.ndim)
print(arr.shape)

2
(2, 3)

# 3차원 배열(텐서)
arr = np.array([[[1, 2, 3], [4, 5, 6]], [[11, 12, 13], [14, 15, 16]]])
print(arr.ndim)
print(arr.shape)

3
(2, 2, 3)

4.1.2.2. 축(axis)

배열에서 데이터를 따라가는 방향
- 차원이 있는 데이터에서 어느 방향으로 연산을 적용하는지 축으로 지정
axis 0은 첫 번째 차원으로, 배열의 가장 바깥쪽 차원임
- 차원이 늘어날수록 새로운 축이 axis=0가 되며, 기존 축들은 번호가 하나씩 뒤로 밀림
축 번호는 배열의 차원에 따라 증가하며, 각 축은 shape에서 해당하는 차원의 크기를 나타냄
- (예) shape (2, 3, 4) → axis 0: 2(면), axis 1: 3(행), axis 2: 4(열)

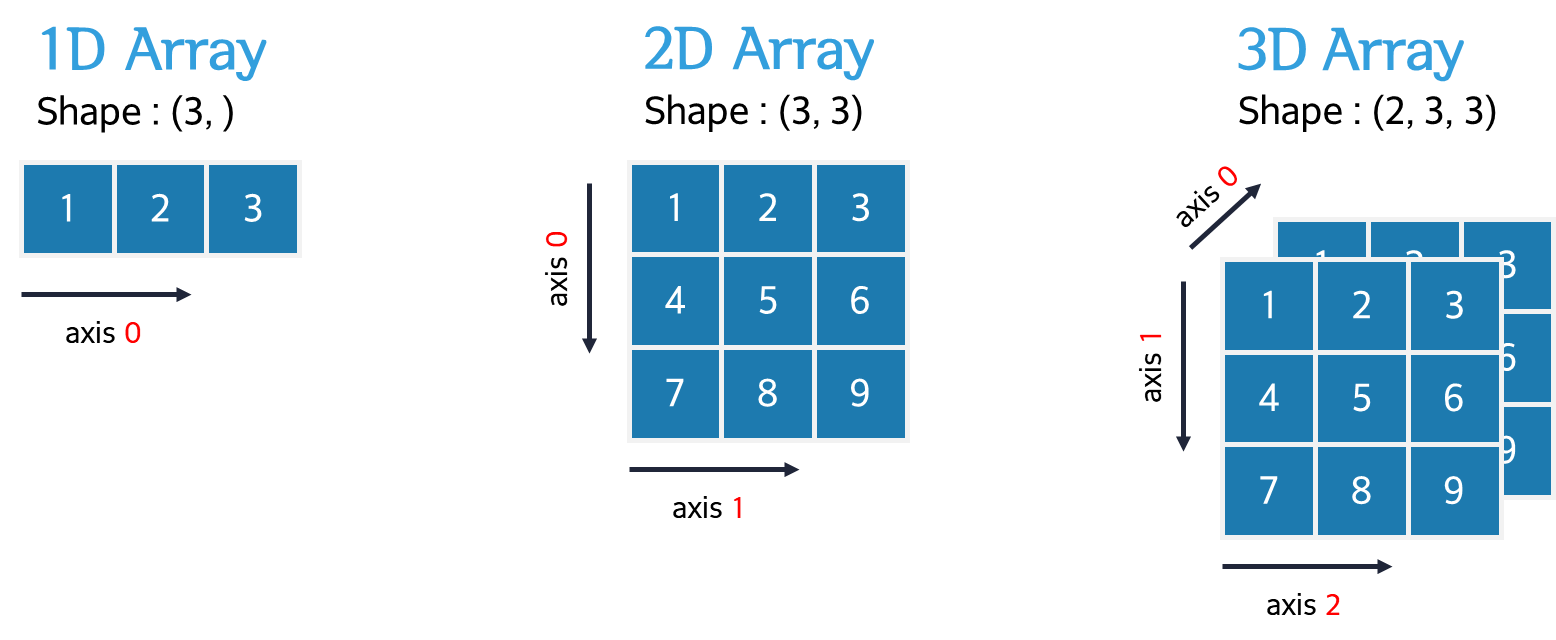
차원	직관적인 구조	축의 역할
1차원	벡터 → [1, 2, 3, 4]	axis 0: 왼쪽 → 오른쪽
2차원	벡터들이 위아래로 쌓임 → 행렬	axis 0: 위 → 아래(행) axis 1: 왼쪽 → 오른쪽(열)
3차원	행렬들이 앞뒤로 쌓임	axis 0: 앞 → 뒤(면) axis 1: 위 → 아래(행) axis 2: 왼쪽 → 오른쪽(열)

4.1.2.3. 넘파이 배열 메소드

함수	설명
sum()	합계
mean()	평균
std()	표준편차
min(), max()	최소값, 최대값
cumsum(), cumprod()	누적 합계, 누적 곱
transpose()	축 순서 변경

arr = np.array([
    [1, 2, 3],
    [4, 5, 6]
])

# 합계
print(np.sum(arr))
print(np.sum(arr, axis=0))
print(np.sum(arr, axis=1))

21
[5 7 9]
[ 6 15]

# 누적합
print(np.cumsum(arr))
print(np.cumsum(arr, axis=0))
print(np.cumsum(arr, axis=1))

[ 1  3  6 10 15 21]
[[1 2 3]
 [5 7 9]]
[[ 1  3  6]
 [ 4  9 15]]

4.1.2.4. 배열 형태 변환

함수	설명
reshape()	배열을 데이터 변경없이 새로운 모양으로 변환
flatten()	다차원 배열을 1차원 배열로 복사하여 반환(원본 유지)
ravel()	다차원 배열을 1차원 배열로 반환(가능하면 원본 공유, 더 효율적)

# 1차원 배열 → 2차원 배열(3행 2열)
arr = np.array([1, 2, 3, 4, 5, 6])

print(arr.reshape(3, 2))
print(arr)                                 # arr 원본 값이 변하지 않음

[[1 2]
 [3 4]
 [5 6]]
[1 2 3 4 5 6]

# 1차원 배열 → 3차원 배열
arr = np.arange(24)

print(arr.reshape(2, 3, 4))
print(arr)                                 # arr 원본 값이 변하지 않음

[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]

 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]

# 2차원 배열 → 1차원 배열 (복사본 반환)
arr = np.array([
    [1, 2, 3],
    [4, 5, 6]
])

print(arr.flatten())
print(arr)                                 # arr 원본 값이 변하지 않음

[1 2 3 4 5 6]
[[1 2 3]
 [4 5 6]]

# 2차원 배열 → 1차원 배열 (가능하면 뷰 반환)
arr = np.array([
    [1, 2, 3],
    [4, 5, 6]
])

print(arr.ravel())
print(arr)                                 # arr 원본 값이 변하지 않음

[1 2 3 4 5 6]
[[1 2 3]
 [4 5 6]]

4.1.2.5. 축 재배열

함수	설명
transpose()	배열의 축 순서 변환(2차원 배열의 경우 행/열 전치)
swaqaxes()	지정한 두 축의 순서를 교환

# 2차원 배열에서 transpose()
arr = np.array([
    [1, 2, 3],
    [4, 5, 6]
])

print(arr.transpose())

[[1 4]
 [2 5]
 [3 6]]

# 3차원 배열에서 transpose()
arr = np.arange(24).reshape(2, 3, 4)

# 축 순서 바꾸기 : (0, 1, 2) → (1, 0, 2)
print(arr.transpose(1, 0, 2))
print(arr.transpose(1, 0, 2).shape)

[[[ 0  1  2  3]
  [12 13 14 15]]

 [[ 4  5  6  7]
  [16 17 18 19]]

 [[ 8  9 10 11]
  [20 21 22 23]]]
(3, 2, 4)

# 3차원 배열에서 axis 0과 axis 2 교환
arr = np.array([
    [[1, 2], [3, 4]],
    [[5, 6], [7, 8]]
])

print(np.swapaxes(arr, 0, 2))
print(np.swapaxes(arr, 0, 2).shape)

[[[1 5]
  [3 7]]

 [[2 6]
  [4 8]]]
(2, 2, 2)

4.1.2.6. 배열 복사

얕은 복사(shallow copy)
- 데이터의 주소를 복사하여 원본과 메모리 공간을 공유
- 원본을 수정하면 복사본이 바뀌며, 반대로 복사본을 수정해도 원본에 영향을 미침
- view(), reshape() (대부분), ravel() (대부분)

깊은 복사(deep copy)
- 완전히 새로운 메모리 공간에 데이터의 복사본을 생성
- 원본을 수정해도 복사본이 바뀌지 않으며, 반대로 복사본을 수정해도 원본에 영향을 주지 않음
- copy(), flatten()

# 얕은 복사
arr = np.arange(6)
print(arr)

copy_arr = arr.view()
print(copy_arr)

copy_arr[0] = 10
print(arr)
print(copy_arr)

[0 1 2 3 4 5]
[0 1 2 3 4 5]
[10  1  2  3  4  5]
[10  1  2  3  4  5]

# 깊은 복사
arr = np.arange(6)
print(arr)

copy_arr = arr.copy()
print(copy_arr)

copy_arr[0] = 10
print(arr)
print(copy_arr)

[0 1 2 3 4 5]
[0 1 2 3 4 5]
[0 1 2 3 4 5]
[10  1  2  3  4  5]

4.1.3. 넘파이 배열 인덱싱과 슬라이싱

인덱싱(indexing)
- [index]를 사용하여 배열의 특정 위치에 있는 원소에 접근함
- 얕은 복사(shallow copy)로 작동 → 원본과 메모리 공간을 공유
- 팬시 인덱싱(fancy indexing)
  - 배열이나 리스트를 인덱스로 사용하여 원하는 위치의 값들을 한 번에 추출
  - 복사본을 반환(deep copy) → 원본과 메모리 공간을 공유하지 않음
- 불리언 인덱싱(boolean indexing)
  - 조건식을 통해 bool형 배열을 생성하여 True인 원소만 추출
  - 복사본을 반환(deep copy) → 원본과 메모리 공간을 공유하지 않음

슬라이싱(slicing)
- [(start index):(stop index)]를 사용하여 배열의 일부 원소를 추출함
- 얕은 복사(shallow copy)로 작동하며 뷰(view)를 반환 → 원본과 메모리 공간을 공유

# 1차원 인덱싱과 슬라이싱
arr = np.array([10, 20, 30, 40, 50])
print(arr[0])
print(arr[-1])
print(arr[1:4])
print(arr[::2])

# 슬라이싱은 기본적으로 뷰(view)임
arr = np.array([10, 20, 30, 40, 50])
print(arr)

sub_arr = arr[1:4]
print(sub_arr)

sub_arr[0] = 100
print(arr)
print(sub_arr)

[10 20 30 40 50]
[20 30 40]
[ 10 100  30  40  50]
[100  30  40]

# copy() 함수를 이용해서 깊은 복사를 해야 원본이 변하지 않음
arr = np.array([10, 20, 30, 40, 50])
print(arr)

sub_arr = arr[1:4].copy()
print(sub_arr)

sub_arr[0] = 100
print(arr)
print(sub_arr)

[10 20 30 40 50]
[20 30 40]
[10 20 30 40 50]
[100  30  40]

# 2차원 인덱싱과 슬라이싱
arr = np.array([[1, 2, 3],
                [4, 5, 6],
                [7, 8, 9]])
print(arr[1, 2])                           # arr[1][2], 리스트에서는 안 됨
print(arr[0:2, 1:3])
print(arr[0])                              # 첫 번째 행의 모든 열
print(arr[:, 1])                           # 모든 행의 두 번째 열
print(arr[1:, :2])                         # 두 번째 행부터 끝까지, 처음부터 두 번째 열까지

6
[[2 3]
 [5 6]]
[1 2 3]
[2 5 8]
[[4 5]
 [7 8]]

# 3차원 인덱싱과 슬라이싱
arr = np.arange(24).reshape(2, 3, 4)

print(arr[1, 2])                           # arr[1][2], 리스트에서는 안 됨
print(arr[1, 2, 3])                        # 두 번째 면, 세 번째 행, 네 번째 열
print(arr[:, 1, :])                        # 모든 면의 두 번째 행 → shape(2, 4)

[20 21 22 23]
23
[[ 4  5  6  7]
 [16 17 18 19]]

# 팬시 인덱싱
arr = np.array([10, 20, 30, 40, 50])
print(arr[[0, 3, 4]])

[10 40 50]

# 불리언 인덱싱
arr = np.array([10, 20, 30, 40, 50])
print(arr > 30)
print(arr[arr > 30])

[False False False  True  True]
[40 50]

4.1.4. 넘파이 배열 연산

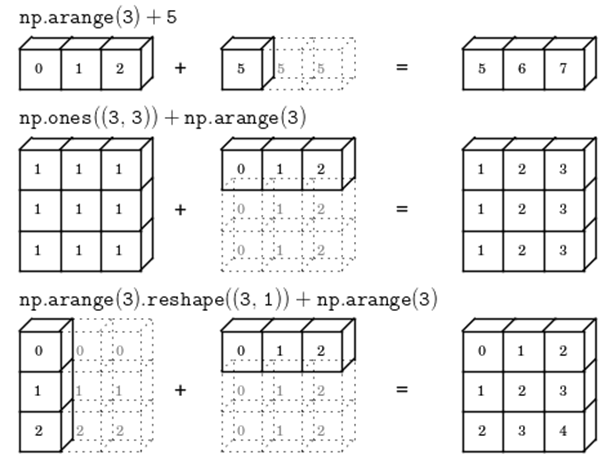
벡터화(vectorization)
- 반복문을 사용하지 않고 배열 전체에 연산을 적용하는 기능
- 동일한 shape을 가진 배열 간에 같은 인덱스에 위치한 원소들끼리(element-wise) 연산을 수행함
- 두 배열의 shape가 다르더라도 브로드캐스팅이 가능한 경우에는 연산이 가능함
  - 이 경우 내부적으로 브로드캐스팅을 통해 shape를 맞춘 후, 벡터화 연산을 수행함

브로드캐스팅(broadcasting)
- 차원이 서로 다른 배열 간의 연산을 자동으로 처리해주는 기능
- 더 작은 차원인 배열의 shape를 자동으로 확장하여 연산이 가능하도록 함
- 브로드캐스팅이 적용되는 조건
  - 차원이 다르면, 더 작은 배열 앞쪽(왼쪽)에 1을 추가해서 맞춰줌
  - 차원이 같으면, 각 차원의 크기를 비교하여 두 값이 같거나 한 쪽이 1이면 브로드캐스팅 가능함

# 벡터화
arr1 = np.array([1, 2, 3])
arr2 = np.array([10, 20, 30])

print(arr1 + arr2)
print(arr1 / arr2)

[11 22 33]
[0.1 0.1 0.1]

# 브로드캐스팅1 : 1차원 + 스칼라
arr = np.array([1, 2, 3])
print(arr + 10)

[11 12 13]

# 브로드캐스팅2 : 차원 수가 다른 경우
arr1 = np.array([[1], [2], [3]])           # shape : (3, 1)
arr2 = np.array([10, 20, 30, 40])          # shape : (4,) → (1, 4)로 간주

print(arr1.shape, arr2.shape)
print(arr1 + arr2)

(3, 1) (4,)
[[11 21 31 41]
 [12 22 32 42]
 [13 23 33 43]]

# 브로드캐스팅3 : 두 배열의 열 크기가 다르므로 브로드캐스팅 불가능
#arr1 = np.array([[1, 2, 3],
#                 [4, 5, 6]])               # shape : (2, 3)
#arr2 = np.array([10, 20, 30, 40])          # shape: (4,) → (1, 4)로 간주
#
#print(arr1.shape, arr2.shape)
#print(arr1 + arr2)

# 브로드캐스팅 : 3차원 + 1차원
arr1 = np.arange(24).reshape(2, 3, 4)      # shape : (2, 3, 4)
arr2 = np.array([10, 20, 30, 40])          # shape : (4,) → (1, 1, 4)로 간주

print(arr1.shape, arr2.shape)
print((arr1 + arr2).shape)                 # shaep : (2, 3, 4)
print(arr1 + arr2)

(2, 3, 4) (4,)
(2, 3, 4)
[[[10 21 32 43]
  [14 25 36 47]
  [18 29 40 51]]

 [[22 33 44 55]
  [26 37 48 59]
  [30 41 52 63]]]